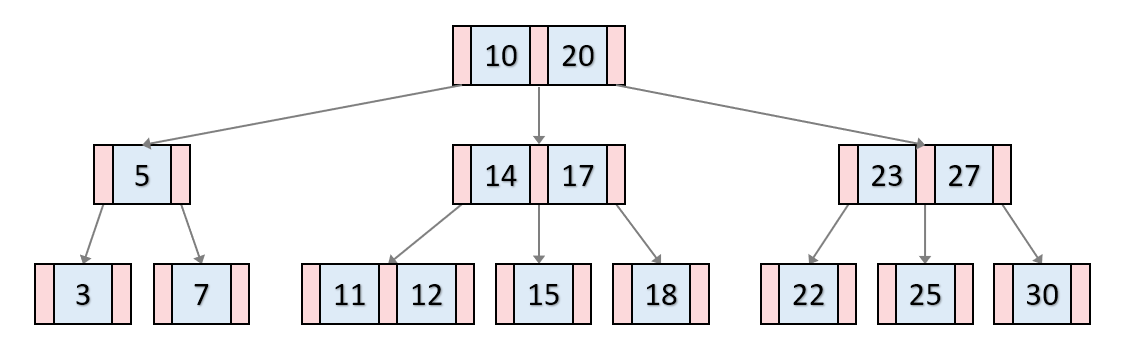
자가 균형 이진 탐색 트리의 일종으로, 데이터베이스와 파일 시스템에서 널리 사용된다.높은 차수의 균형 트리로, 각 노드가 여러 자식을 가질 수 있다.모든 리프 노드는 동일한 레벨에 존재하기 때문에, B 트리는 O(logN)의 시간 복잡도를 갖는다. 특징각 노드는 최대 M개의 자식을 가질 수 있다. 이러한 트리를 M차 B 트리라고 부른다.루트 노드를 제외한 모든 노드는 최소 ⌈M/2⌉개의 자식을 가져야 한다.노드는 데이터와 포인터로 구성되며, 데이터는 오름차순으로 정렬되어 있다. 정렬된 순서에 따라 자녀 노드들의 키 값의 범위가 결정된다.각 노드는 최대 ⌈M/2⌉ - 1개에서 최대 M - 1개의 키를 가질 수 있다. 데이터 삽입삽입은 항상 리프 노드에서 시작한다.해당 리프 노드에 여유 공간이 있다면 데이터..